➡️ 카이제곱 분포와 계산식
- 카이제곱 분포 : 범주형 데이터의 독립성 검정이나 적합도 검정에 사용되는 분포
- 카이제곱( \chi^2, chi-square) : (관측값-예측치)^2 / 기대값 의 합

- 관측값이 클수록 (=관측값-기대값의 차이가 클수록) 카이 제곱 통계량이 우측으로 이동함 → 값이 희귀해짐 → 귀무가설을 기각할 가능성이 높아짐
- 자유도가 클수록 카이제곱 분포가 우측으로 확장됨
- 자유도가 작을수록 0근처에 몰려있음
- 자유도가 증가하면 분포가 넓어지고,평균이 우측으로 이동하고, 오른쪽 꼬리가 길어짐 → 점점 정규 분포 근사

➡️ 카이제곱 검정 (Chi-Square Test)
- 비모수 검정
- 전제 조건 : 정규분포를 안 따라도 됨 / 각 카테고리 빈도수는 5개 이상 이여야함. ( 거의 충족 됨 )
- 카이제곱 검정 : 범주형 데이터의 분포나 관계를 분석하기 위해 사용하는 검정 법
➡️ 카이제곱 검정 - 적합도 검정 (1차원)
- 기대비율과 관찰비율의 차이를 검정 (기대분포와 실제분포가 일치하는지)
- 표본 (1차원) : 몇개의 범주로 분류된 1개의 표본
- 적합도 검정의 기대값 계산(E) :
기대확률 * 전체 관측값의 합

- 적합도 검정 예시
- 요일별 방문 고객수 비율 적합도 검정
- 배경 : 요일별 방문 고객수 비율은 아래와 같음. 최근 변동이 있어 기존 비율이 깨졌는지 검정 하고자 함
- 가설
- 귀무 : 기존 비가 맞다
- 대립 : 기존 비가 아니다
- 결과
- 카이제곱 통계량 : 11.442
- 자유도 : 5 (n-1)
- p-value는 0.043
- 유의수준 0.05 보다 작으므로 귀무가설은 기각됩니다.
- 따라서, 각 요일별 방문자 수의 비가 기존에 알려진 것과 다름


- 코드 구현
더보기
- 자유도가 5인 카이제곱 분포와 검정통계량 코드
# 기존 방문 비율(%)을 기반으로 기대값을 계산
expected_ratios = np.array([10, 10, 15, 20, 30, 15])
total_visits = 200
expected_counts = (expected_ratios / 100) * total_visits
# 관찰된 방문 수
observed_counts = np.array([30, 14, 34, 45, 57, 20])
# 카이제곱 적합도 검정을 수행
chi2_stat, p_val = stats.chisquare(f_obs=observed_counts, f_exp=expected_counts)
# 결과 출력
print(f"Chi-squared Statistic: {chi2_stat:.3f}") # 11.442
print(f"P-value: {p_val:.3f}") # 0.043
# 결론 도출
alpha = 0.05 # 유의수준
if p_val < alpha:
print("귀무가설 기각: 관찰된 방문 비율은 기존 비율과 다르다.")
else:
print("귀무가설 채택: 관찰된 방문 비율은 기존 비율과 같다.")
'''
Chi-squared Statistic: 11.442
P-value: 0.043➡️ 카이제곱 검정 - 독립성 검정 (2차원)
- 두 카테고리의 독립유무를 검정
- 표본 (2차원) : 1개의 표본을 2가지 특성으로 분류
- 2원 분할표에서 자유도 :
(행의수-1 )*(열의수 -1) - 적합도 검정의 기대값 계산(E) :
행 합계*열 합계/ 전체 관측값의 합

- 독립성 검정 예시
- 성별과 흡연여부에 대한 독립성 검정
- 배경 : 표본의 두가지 특성이 연관이 있나 없나
- 가설
- 귀무 : 성별과 흡연은 독립적임
- 대립 : 성별과 흡연은 독립적이지 않음 (= 연관이 있음)
- 결과
- 카이제곱 통계량 : 2.1978
- 자유도 : 1
- p-value는 0.138
- 유의수준 0.05 보다 크므로 귀무가설 채택
- 따라서, 성별과 흡연유무는 독립적임

➡️ 카이제곱 검정 - 동질성 검정 (2차원)
- 두 집단의 분포가 동일한지 검정 = N개의 그룹이 각 범주별로 동일한 반응을 보이는가?
- 표본 (2차원) : 몇개의 범주로 분류된 N개의 독립 표본
- 2원 분할표에서 자유도 :
(행의수-1 )*(열의수 -1) - 적합도 검정의 기대값 계산(E) :
행 합계*열 합계/ 전체 관측값의 합(독립성과 동일) - 동질성 검정 예시
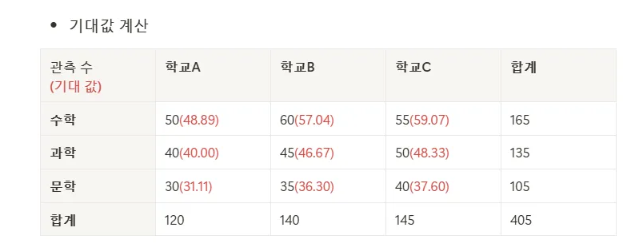
- 각 학교별 과목 선호도에 대한 동질성 검정
- 배경 : 각 학교별 과목 선호도가 동일하냐 아니냐
- 가설
- 귀무 : 각 학교의 과목의 선호도는 동일하다.
- 대립 : 각 학교의 과목의 선호도는 동일하지 않다
- 결과
- 카이제곱 통계량 : 0.87
- 자유도 : 4
- p-value는 : 0.936
- 유의수준 0.05 보다 크므로 귀무가설 채택
- 따라서, 학교별 과목 선호도는 동일함
➡️ 독립성과 동질성 비교
- 두 검정은 동일한 chisquare 검정을 진행
- 단지 검정의 목적과 해석의 차이가 존재
- 목적
- 독립성 : 두 범주형 변수간의 독립 유무
- 동질성: 여러 집단에서 동일한 범주의 분포 확인
- 가설
- 독립성의 귀무가설 : 두 변수는 독립적임
- 동질성의 귀무가설 : 모든 그룹의 분포가 동일
➡️ 카이제곱 검정 코드 구현
- 적합도 검정 :
stats.chisquare(관찰값, f_exp=기대값)
더보기
- 기대값 계산
- 카이제곱 검정 수행 : chisquare ( 관찰값, 기대값) 파라미터로 받음 :1차원
- 결과 출력
import numpy as np
import scipy.stats as stats
# 주장하는 방문 비율(%)을 기반으로 기대값을 계산
expected_ratios = np.array([10, 10, 15, 20, 30, 15])
total_visits = 200
expected_counts = (expected_ratios / 100) * total_visits
# 관찰된 방문 수
observed_counts = np.array([30, 14, 34, 45, 57, 20])
# 카이제곱 적합도 검정을 수행
chi2_stat, p_val = stats.chisquare(f_obs=observed_counts, f_exp=expected_counts)
# 결과 출력
print(f"Chi-squared Statistic: {chi2_stat:.3f}") # 11.442
print(f"P-value: {p_val:.3f}") # 0.043
# 결론 도출
alpha = 0.05 # 유의수준
if p_val < alpha:
print("귀무가설 기각: 관찰된 방문 비율은 주장하는 비율과 다르다.")
else:
print("귀무가설 채택: 관찰된 방문 비율은 주장하는 비율과 같다.")- 독립성/동질성 검정 :
stats.chi2_contingency(df)
더보기
- 카이제곱 검정 수행 : chi2_contingency (df ) 파라미터로 받음 :2차원
- 결과 출력
# 관찰된 데이터: 성별과 흡연 여부에 따른 빈도수
data = np.array([
[40, 60], # 남성: 흡연자, 비흡연자
[30, 70] # 여성: 흡연자, 비흡연자
])
# 카이제곱 통계량, p-value, 자유도, 기대값을 계산
chi2_stat, p_val, dof, expected = stats.chi2_contingency(data, correction=True)
# 결과 출력
print(f"Chi-squared Statistic: {chi2_stat:.3f}") #1.780
print(f"P-value: {p_val:.3f}") #0.182
print(f"Degrees of Freedom: {dof:.3f}") #1.000
print("Expected frequencies:")
print(expected)
'''
[[35. 65.]
[35. 65.]]
'''
# 결론
alpha = 0.05 # 유의수준
if p_val < alpha:
print("귀무가설 기각: 성별과 흡연 여부는 독립적이지 않다.")
else:
print("귀무가설 채택: 성별과 흡연 여부는 독립적이다.")'통계,검정,머신러닝' 카테고리의 다른 글
| 머신러닝 실습 | 캐글의 Titanic 데이터로 로지스틱 회귀 분석 실습 하기 (+K fold 교차검증) (0) | 2025.01.15 |
|---|---|
| 머신러닝 | 이상치/ 결측치/ 범주형 데이터 인코딩/ 수치형 데이터 스케일링(+sklearn 모듈) (0) | 2025.01.15 |
| 통계 기초 | 오류의 종류와 오류 보정법(+본페르니 보정 코드 ) (0) | 2025.01.14 |
| 머신러닝 | 로지스틱 회귀 분석/분류 분석 (+sklearn 파이썬 실습) (1) | 2025.01.14 |
| 머신러닝 | 머신러닝 기초와 선형 회귀 분석 (+sklearn 파이썬 실습) (0) | 2025.01.13 |
