검정 | 통계적 가설 검정 실습1 (T검정/ 카이제곱 검정)

성장하는 쿠키의 로그 기록 2025. 1. 24. 22:55

☑️ 필수 1. 기초 통계

[문제]

statistics csv 파일을 읽고, 성별 Review Rating 에 대한 평균과 중앙값을 동시에 구해주세요. 결과는 소수점 둘째 자리까지 표현해주세요.
그리고 이에 대한 해석을 간략하게 설명해주세요.

[문제 풀이]

내 코드

import pandas as pd
import numpy as np 
import scipy.stats as stats
from datetime import datetime, timedelta
import matplotlib.pyplot as plt
import seaborn as sns

df=pd.read_csv('statistics.csv')
df.groupby('Gender')['Review Rating'].agg(['mean','median']).round(2)

피드백 및 결과 해석

성별 review rating의 평균과 중앙값 df형태로 추출
agg 메소드
- 다양한 집계값 출력시 리스트로 전달 → agg(['함수1','함수2'])
- 컬럼별 다른 집계값 적용시 딕셔너리로 전달 → agg({'total_bill': 'max','tip': 'sum'})
결과 해석 : 성별간 평균값과 중앙값이 거의 차이가 없음
- (내 해석 오류) 남성이 여성보다 평균 (+0.01p) 중앙값 (+0.1p) 으로 미약하지만 남성의 중앙값이 더 우측으로 치우쳐져 있으므로 '남성의 리뷰점수가 여성대비 더 높은 경향이 있다'
- (피드백) : 내 해석은 확대 해석되었음. 표본 데이터의 평균과 중앙값의 차이가 있어도, 아주 살짝분포가 다를뿐 그게 남녀의 리뷰주는 것 에대해 분포가 다르다는 증거가 되지 못함. → 그래서 검정 과정이 후행 되어야함
조건별 데이터 필터링 ( `암묵적 체이닝` vs `loc` )
- 성별(조건별) 컬럼 필터링 -> loc 권장, 암묵적 체이닝은 오류 있을수있음

#1) 암묵적 체이닝 -> df[조건][컬럼] 
male = df[df['Gender'] == 'Male']['Review Rating']

#2) loc 사용 
con = df['Gender'] == 'Male'
male_df = df.loc[con,'Review Rating']

시각화

# 성별 히스토그램으로 분포 비교해보기
male = df[df['Gender'] == 'Male']['Review Rating']
female = df[df['Gender'] == 'Female']['Review Rating']

plt.figure(figsize = (4,3))
plt.hist(male)
plt.hist(female)
plt.xlim(0,5) #MIN-MAX 범위가 동일함 
plt.show()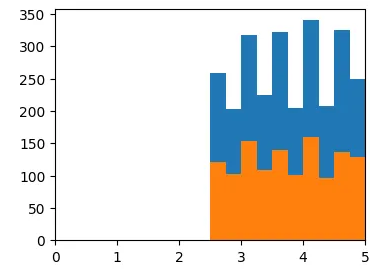

한줄 포인트

여러 방식으로 집계시 리스트로 전달 → agg(['함수1','함수2'])
표본 집단의 기술통계치(점 추정) 만으로 모집단을 설명할 수없음 → 검정 추가 진행 (전체 고객의 데이터가 아닌 이상 all 표본 데이터)

☑️ 필수 2. 통계적 가설검정

[문제]

성별, Review Rating 컬럼에 대한 T-TEST 를 진행해주세요.
- 해당 데이터셋의 컬럼들은 정규성을 만족한다고 가정하겠습니다.
- 귀무가설과 대립가설을 작성해주세요.
- t-score, P-value 를 구해주세요.
그리고 이에 대한 귀무가설 채택/기각 여부와 그렇게 생각한 이유를 간략하게 설명해주세요.

[문제 풀이]

내 코드

import pandas as pd
import numpy as np 
import scipy.stats as stats
from datetime import datetime, timedelta
import matplotlib.pyplot as plt
import seaborn as sns

# 2표본 t검정, 정규성 만족, 성별은 두표본은 독립적임 
con = df['Gender'] == 'Male'
male_df = df.loc[con,'Review Rating']

con = df['Gender'] == 'Female'
female_df = df.loc[con,'Review Rating']

alpha=0.05
t_score, p_val = stats.ttest_ind(male_df,female_df) 

print('귀무가설 : 성별간 리뷰점수는 차이가 없다') #리뷰점수는 같다 , 독립이 아니다 
print('대립가설 : 성별간 리뷰점수는 차이가 있다')
print(f't-score: {t_score:.3f}, P-value : {p_val:.3f}')

if p_val < alpha:
    print('귀무가설을 기각합니다. 성별간 리뷰 점수는 차이가 있습니다.')
else:
    print('귀무가설을 채택합니다. 성별간 리뷰 점수는 차이가 없습니다.')

피드백 및 결과 해석

T 검정 조건
- 모 표준편차 모름
- 정규성 만족 (표본 크기가 상관없음) OR 표본크기가 30개 이상 (중심극한 정리)
2표본 T검정 조건
- 독립 표본
- 정규성 검정
- 등분산성
  - 등분산 검정 o : stats.ttest_ind (a,b,equal_var=True) -- 디폴트
  - 등분산 검정 x : stats.ttest_ind (a,b,equal_var=False)
  - 등분산 검정
    - 귀무: 각 그룹의 분산을 모두 동일하다 (등분산 만족)
    - 대립 : 적어도 하나의 분산이 다르다.
    - `Levenu` : 정규성 검정 스킵가능, 여러 그룹의 분산이 동일한지 확인
    - `Bartlett` : 정규성 만족 시 사용, `Levenu`보다 검정력이 높음

#Levene 등분산 검정 코드
_, p_value = stats.levene(a, b)

print(f'{p_value:.3f}')
if p_value < 0.05:
    print('대립가설 채택: 적어도 하나의 분산이 다름')
else:
    print('귀무가설 채택, 분산이 같음')

문제에서 정규성 만족 but 등분산성 정보는 없으므로 등분산성 검정 선행 해주어야 함

한줄 포인트

2표본 t검정 진행시, 전제 조건3가지 사전 확인 필수 ( 독립 변수, 정규성,등분산성)
등분산성 가정이 어렵다면 ttest_ind 메소드 사용시 equal_var =False 옵션 활용 할것

☑️ 필수 3. 통계적 가설검정2

[문제]

Color, Season 컬럼에 대한 카이제곱 검정을 진행해주세요.
- 귀무가설과 대립가설을 작성해주세요.
- 두 범주형 자료의 빈도표를 만들어주세요. 이를 코드로 작성하여 기재해주세요.
- 카이제곱통계량, P-value 를 구해주세요.
그리고 이에 대한 귀무가설 채택/기각 여부와 그렇게 생각한 이유를 간략하게 설명해주세요.

[문제 풀이]

내 코드

#가설 설정
print('귀무가설 : 제품 컬러와 구매 시즌은 독립적이다')
print('대립가설 : 제품 컬러와 구매 시즌은 독립적이지 않다')

df_chi.groupby('Season')['Color'].count()

#피벗해서 빈도표 생성
observed = df_chi.pivot_table(index='Color', columns='Season', aggfunc='size')
display(observed)

# 독립성 검정
alpha=0.05
chi2_stat, p_val2, dof, expected = stats.chi2_contingency(observed)

print(f"독립성 검정 카이제곱 통계량: {chi2_stat:.3f}, p-value: {p_val2:.3f}\n")

if p_val2 < alpha:
    print('귀무가설을 기각 : 제품 컬러와 구매 시즌은 관련이 있습니다.')
else:
    print('귀무가설을 채택 :제품 컬러와 구매 시즌은 관련이 없습니다.')

피드백 및 결과 해석

카이제곱 검정법
- 적합도 검정 : 기대만큼 관측되었는가? -> 1차원 변수, 변수가 2이상이면 적용불가
- 독립성 검정 : 두 변수가 연관이 있는가? -> 두 변수의 연관성 파악
- 동질성 검정 : 변수들의 분포가 같은가 ? -> 계절에 따라 구매분포가 같은가 다른가.
교차표 (빈도표 생성 ) 시 `crosstab` 함수나 `pivot_table` 함수 활용가능

#1. 피벗(그룹바이 후 -> 피벗)
df_chi.groupby('Season')['Color'].count()
observed = df_chi.pivot_table(index='Color', columns='Season', aggfunc='size')

#2. crosstab 함수 생성
color = df['Color'] #x축
season = df['Season'] #y축
data = pd.crosstab(index=color,columns=season)

독립성 검정 가설
- 귀무 : 두 변수는 독립적이다 = 두 변수는 연관이 없다
- 대립 : 두 변수는 독립적이지 않다 = 두 변수는 관련이 있다

한줄 포인트

카이제곱 검정 (독립/종속 변수가 범주형) 시, 변수가 1개 → 적합도 검정, 변수가 2개 → 독립/동질성 검정
독립/동질성 검정은 함수 방식은 동일하나 목적/해석의 차이가 있음
2원 분할표등 교차표 생선시 `crosstab` 함수 사용