통계 실습2 | 카이제곱 검정 /분포별 난수로 샘플 생성하기 / 중심극한정리 (+subplots/subplot 시각화)

통계,검정,머신러닝

통계 실습2 | 카이제곱 검정 /분포별 난수로 샘플 생성하기 / 중심극한정리 (+subplots/subplot 시각화)

성장하는 쿠키의 로그 기록 2025. 1. 18. 00:49

☑️ 문제4. 카이제곱 검정

[문제]

- 다음 `click_rate` 데이터는 헤드라인별 클릭과 클릭하지 않은 수 에 대한 데이터입니다.

- 귀무가설과 대립가설을 설정하세요.

- 카이제곱 검정 수행하여 실제로 클릭률에 대한 차이가 있는지 유의수준 0.05 에서 검정해보세요.

[문제 풀이]

내 코드 -오답

import pandas as pd
from scipy import stats
# URL 로 데이터 가져오기
url = "https://raw.githubusercontent.com/gedeck/practical-statistics-for-data-scientists/master/data/click_rates.csv"
click_rate  = pd.read_csv(url)
clicks = click_rate.pivot(index='Click', columns='Headline', values='Rate')
display(clicks)

print('귀무가설 : 헤드라인과 페이지 클릭률은 동일하다.')
print('대립가설 : 헤드라인과 페이지 클릭률은 동일하지 않다.')

chi2_stat, pvalue, dof, expected = stats.chi2_contingency(clicks, correction=True)
print(f'chisq: {chi2_stat:.3f}')
print(f'pvalue: {pvalue:.3f}')

# 결론
alpha = 0.05  # 유의수준
if pvalue < alpha:
    print("귀무가설 기각: 헤드라인과 페이지 클릭률은 관련이 있다.")
else:
    print("귀무가설 채택: 헤드라인과 페이지 클릭률은 관련이 없다.")

수정 코드 -카이제곱 함수 correction=True 옵션 적용

import pandas as pd
from scipy import stats
# URL 로 데이터 가져오기
url = "https://raw.githubusercontent.com/gedeck/practical-statistics-for-data-scientists/master/data/click_rates.csv"
click_rate  = pd.read_csv(url)
clicks = click_rate.pivot(index='Click', columns='Headline', values='Rate')
display(clicks)

print('귀무가설 : 헤드라인별 클릭률은 동일하다')
print('대립가설 : 헤드라인별 클릭률은 동일하지 않다')
chi2_stat, pvalue, dof, expected = stats.chi2_contingency(clicks)
print(f'chisq: {chi2_stat:.3f}')
print(f'pvalue: {pvalue:.3f}')

# 결론
alpha = 0.05  # 유의수준
if pvalue < alpha:
    print("귀무가설 기각: 헤드라인과 페이지 클릭률은 관련이 있다.")
else:
    print("귀무가설 채택: 헤드라인과 페이지 클릭률은 관련이 없다.")

이슈 및 해결 과정

검정법 선택 아이디어
- 종속변수가 click or not click 이산형이고
- 각 범주의 빈도가 5이상 이기때문에 카이제곱 검정 진행
- 5미만일 경우 fisher's 검정 사용 → `scipy.stats.fisher_exact()`
  - but 5미만이면 데이터를 더 수집하는게 나음

2×2 분할표이고, 기대빈도가 5 미만	Fisher의 정확 검정
2×2 분할표이고, 카이제곱 검정을 그대로 쓰고 싶음	Yates 보정된 카이제곱 검정
범주 개수가 2개 이상이고, 기대빈도가 작은 경우	G-검정

카이제곱 독립성/동질성 검정 : 'chi2_contingency`
- 반환값 : 검정 통계량, p값,자유도,기대값 (리스트)
- correction = True : 자유도가 1일때 수치 보정해주는 옵션임
  - 즉, 자유도가 1인 2X2 미만 일때 사용
  - 디폴트는 False
  - 문제는 3x2이기때문에 자유도2 옵션 설정 안해도 됨
chi2_stat, pvalue, dof, expected = stats.chi2_contingency(clicks)

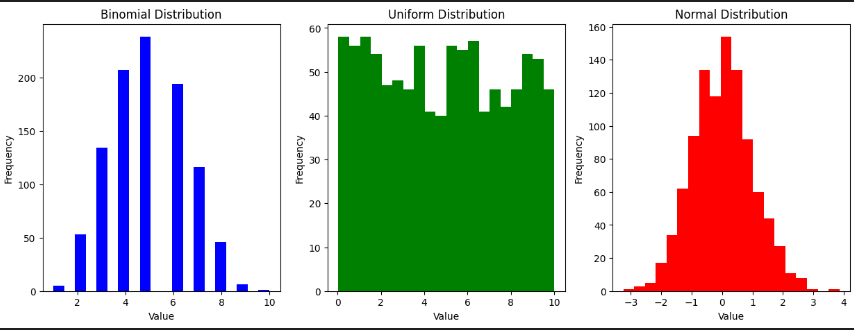
☑️ 문제5. 이항분포/균등분포/표준 정규분표 난수 추출 후 시각화

[문제]

- `scipy.stats` 모듈에서 다음 분포를 생성하고 히스토그램으로 표현하기(subplots권장)

- 변수

- 이항 분포 샘플 변수명 `binomial_data`: 확률 0.5의 시행을 10번 시행했을때 성공할 갯수의 1000개의 표본 생성

- ex 동전 10번 던졌을때 앞면이 나올 수 있는 수는 0부터 10개

- 균등 분포 샘플 변수명 `uniform_data` : 시작 0, 끝 10의 표본 1000개 생성

- 표준 정규 분포 샘플 변수명 `normal_data` : 표본 1000개 생성

- 위 분포 3개를 히스토그램으로 표현하되 `plt.subplots(1,3)`을 이용하여 동시에 표현하고, `bins` 는 20개로 설정

[문제 풀이]

내 코드

import scipy.stats as stats 
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

# scipy를 통한 샘플 생성
binomial_data = stats.binom.rvs(n=10, p=0.5, size=1000,random_state=None)  #이항분포 샘플 생성
uniform_data = stats.uniform.rvs(0,10,size=1000,random_state=None)
normal_data = stats.norm.rvs(size=1000,random_state=None) #정규분포 난수 생성 (표준 정규분포임,loc=0 scale=1가 디폴트)

#시각화
fig,axs = plt.subplots(1,3,figsize=(15, 5)) #subplots 사용법 subplots(행,열,figure=(가로,세로))

axs[0].hist(binomial_data,bins=20,color='blue') #히스토그램 생성 
axs[0].set_title('Binomial Distribution') #타이틀 

axs[1].hist(uniform_data,bins=20,color='green')
axs[1].set_title('Uniform Distribution')

axs[2].hist(normal_data,bins=20,color='red')
axs[2].set_title('Normal Distribution')

for ax in axs:
    ax.set(xlabel='Value',ylabel='Frequency')

수정 코드

import matplotlib.pyplot as plt
from scipy.stats import * #binom, norm, uniform

sample_size = 1000
uniform_data = uniform.rvs(loc= 0, scale = 10, size = sample_size)
binomial_data = binom.rvs(n = 10, p = 0.5, size = sample_size)
normal_data = norm.rvs(loc = 0, scale = 1, size = sample_size)

#시각화
plt.figure(figsize=(15, 5))

plt.subplot(1, 3, 1)
plt.hist(binomial_data, bins=20, color="blue", alpha=0.7)
plt.title("Binomial Distribution")
plt.xlabel("Value")
plt.xticks(range(0,11))
plt.ylabel("Frequency")

plt.subplot(1, 3, 2)
plt.hist(uniform_data, bins=20, color="green", alpha=0.7)
plt.title("Uniform Distribution")
plt.xlabel("Value")
plt.ylabel("Frequency")
plt.xticks(range(0,11))

plt.subplot(1, 3, 3)
plt.hist(normal_data, bins=20, color="red", alpha=0.7)
plt.title("Normal Distribution")
plt.xlabel("Value")
plt.ylabel("Frequency")

plt.tight_layout()
plt.show()

이슈 및 해결 과정

각 분포를 따르는 샘플 생성(난수)
- 이항분포 : stats.binom.rvs(n=10, p=0.5, size=1000,random_state=42)
  - n= 시행횟수, p= 확률 size =표본갯수
  - random_state=랜덤 시드 고정여부 → random_state=42 (고정), random_state=None (랜덤/디폴트)
- 균등분포 :stats.uniform.rvs(0,10,size=1000,random_state=42)
- 표준정규분포 :stats.norm.rvs(size=1000,random_state=42)
subplots 시각화
- 한번에 생성 → 객체로 접근
  - plt.subplots (행,열,figure=(가로,세로))
  - fig,axs = plt.subplots(1,3,figsize=(15, 5))
  - subplots 반환값 : figure(프레임) , 객체
  - ex) 첫번째 차트에 시각화 : axs[0]
    - axs[0].hist(binomial_data,bins=20,color='blue')
subplot 시각화
- plt.figure(figsize=(가로,세로)) : 캔버스 생성
- plt.subplot (행,열, 인덱스) : 인덱스에 각각 시각화
- plt.figure(figsize=(15, 5))
  
  plt.subplot(1, 3, 1)
  
  plt.hist(binomial_data, bins=20, color="blue", alpha=0.7)
- ex) 첫번째 차트에 시각화 : plt.subplot(1,3,1)

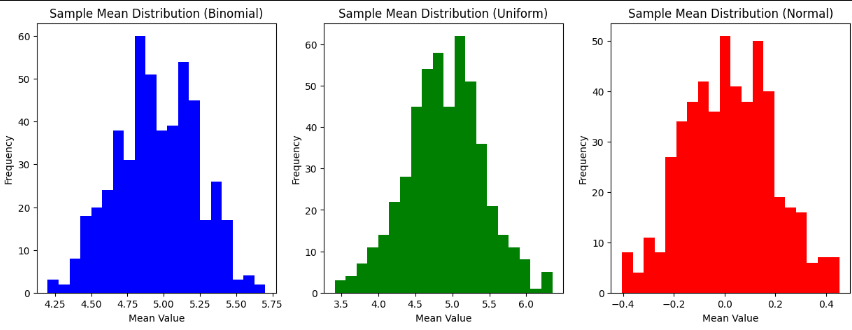
☑️ 문제6. 이항분포/균등분포/표준 정규분표 중심극한 정리 후 시각화 (부트 스트래핑)

[문제]

- `numpy.choice` 함수를 이용하여 각 분포 평균을 내고 이를 500번 반복하여 표본 평균을 생성해 봅시다. (ex `bionmial_data` 에서 30개씩 뽑아 500번 반복)

- 표본의 평균들을 히스토그램으로 시각화여 정규분포를 따르는지 확인해봅시다.

- 변수

- `num_samples` : 표본추출할 횟수

- `sample_means`: 딕셔너리 자료형으로 **Binomal**, **Uniform**, **Normal** 의 Key값을 가지며 해당하는 values들은 각 30개씩 복원추출하여 뽑은 샘플의 평균 값을 저장. 이를 총 500번 진행

[문제 풀이]

내 코드 -오답

import scipy.stats as stats 
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
# import random

# scipy를 통한 샘플 생성
binomial_data = stats.binom.rvs(n=10, p=0.5, size=1000,random_state=42)  #이항분포 샘플 생성
uniform_data = stats.uniform.rvs(0,10,size=1000,random_state=42) #난수 생성할껀데 0-10사이값으로 
normal_data = stats.norm.rvs(size=1000,random_state=42) #정규분포 난수 생성 

#표본의 평균을 모아야하는데 딕셔너리로 간단하게 표현 
sample_means = { # 밸류들은 30개씩 복원 추출하여 뽑은 샘플의 평균값을 저장할 딕셔너리
    "Binomial": [],
    "Uniform": [],
    "Normal": []
}

#랜덤 30개 추출 후 평균냄 -> 딕셔너리 키 값으로 저장 -> 500회 반복 -> 해당 어레이 시각화 
num_samples = 500 # 표본추출횟수
n=0
while n < num_samples:
    sample_means["Binomial"].append(np.random.choice(binomial_data,size=30,replace=False).mean())
    sample_means["Uniform"].append(np.random.choice(uniform_data,size=30,replace=False).mean())
    sample_means["Normal"].append(np.random.choice(normal_data,size=30,replace=False).mean())
    n+=1

#시각화
fig,axs = plt.subplots(1,3,figsize=(15, 5)) #subplots 사용법 subplots(행,열,figure=(가로,세로))

axs[0].hist(sample_means["Binomial"],bins=20,color='blue') #히스토그램 생성 
axs[0].set_title('Sample Mean Distribution (Binomial)') #타이틀 

axs[1].hist(sample_means["Uniform"],bins=20,color='green')
axs[1].set_title('Sample Mean Distribution (Uniform)')

axs[2].hist(sample_means["Normal"],bins=20,color='red')
axs[2].set_title('Sample Mean Distribution (Normal)')

for ax in axs:
    ax.set(xlabel='Mean Value',ylabel='Frequency')

이슈 및 해결 과정

중심극한 정리 사용을 위해 30개씩 복원추출로 500번 반복
- while 반복문 적용 :
  - num_samples = 500 # 표본추출횟수
    
    n=0
    
    while n < num_samples:
    
    sample_means["Binomial"].append(np.random.choice(binomial_data,size=30,replace=True).mean())
    
    sample_means["Uniform"].append(np.random.choice(uniform_data,size=30,replace=True).mean())
    
    sample_means["Normal"].append(np.random.choice(normal_data,size=30,replace=True).mean())
    
    n+=1
- for 반복문 적용 :
  - num_samples = 500
    
    for _ in range(num_samples):
    
    sample_means["Binomial"].append(np.mean(np.random.choice(binomial_data, size=30, replace=True)))
    
    sample_means["Uniform"].append(np.mean(np.random.choice(uniform_data, size=30, replace=True)))
    
    sample_means["Normal"].append(np.mean(np.random.choice(normal_data, size=30, replace=True)))
- np.random.choice : 리스트에서 랜덤 추출해주는 메소드
  - replace 옵션 : 복원 / 비복원 추출
    - replace= True : 복원
    - reaplace= False : 비복원
- 평균 구할때
  - 1번째 : np.random.choice(변수).mean()
  - 2번째 : np.mean(np.random.choice(변수)
  - 둘다 가능하나, 2번이 더 직관적임

https://kr.matplotlib.net/stable/gallery/subplots_axes_and_figures/subplots_demo.html#google_vignette

plt.subplots를 사용하여 여러 서브플롯 만들기_Matplotlib - Python 시각화

메모 전체 예제 코드를 다운로드 하려면 여기 를 클릭 하십시오. 을 사용하여 여러 서브플롯 만들기plt.subplots pyplot.subplots단일 호출로 그림과 서브플롯 그리드를 생성하는 동시에 개별 플롯이 생

kr.matplotlib.net

https://kr.matplotlib.net/stable/gallery/subplots_axes_and_figures/subplots_demo.html

plt.subplots를 사용하여 여러 서브플롯 만들기_Matplotlib - Python 시각화

kr.matplotlib.net