➡️ 모집단 & 표본
- 우리의 목표는 표본으로 모집단을 얼마나 정확하게 추정 할수있는지가 핵심
- 모집단 : 전체 집단
- 표본 : 모집단에서 추출한 일부 샘플
- 표본 추출의 중요성 : 제대로 샘플링하 하지 않으면 샘플링 편향이 일어날 수 있음
- 표본의 표준편차/분산에는 자유도 (n-1) 개념이 들어감. 표본의 표준편차및 분산 계산시 n-1로 나눠줌
▼모집단 & 표본 히스토그램 시각화 코드 구현
더보기
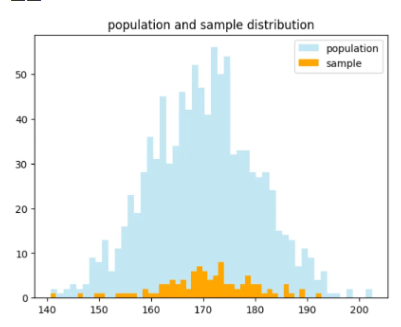
- 모집단 과 표본 히스토그램 시각화

import numpy as np
import matplotlib.pyplot as plt
# 모집단 생성 (예: 국가의 모든 성인의 키 데이터)
population = np.random.normal(170, 10, 1000) #평균이170 표쥰편차가 10인 1000개 정규분포 샘플 생성
# 표본 추출
sample = np.random.choice(population, 100)
plt.hist(population, bins=50, alpha=0.5, label='population', color='blue')
plt.hist(sample, bins=50, alpha=0.5, label='sample', color='red')
plt.legend()
plt.title('population and sample distribution')➡️자유도
- 표본의 불편추정량을 구할때 사용(모집단에는 적용되지않음)
- 자유도 : 어떤 식에서 독립변수를 자유롭게 선택할 수 있는 경우의 수
- ex a+b+c =10 이고, a=5 b=2 이면 c는 3일수 밖에 없음. 즉, `자유도 2`
- 편차의 합이 0 이 되는경우 = 평균이 데이터의 딱 중심에 있다. (평균이 올바르게 구해졌다)
- 편차의 합을 0으로 만들기 위해 자유롭게 선택할수있는 독립 변수의 갯수는 n-1개 임 즉, `자유도 : n-1`

➡️ 표본 오차 와 신뢰구간
- 표본 오차 : 표본에서 계산된 통계량(즉, 추정값)과 모집단의 진짜 값 간의 차이
- 표본의 크기가 클수록 표본오차는 작아짐(데이터가 많을수록 모집단을 더 잘 대표하게 됨)
- 무작위 추출 방법을 사용하면 표본 오차를 줄일수있음.
- ✅ 표본 표준오차 계산 : 표준편차를 표본 크기의 제곱근으로 나눈 값
- 신뢰 구간 : 모집단의 특정값(평균,분산 등)에 추정한 값이 포함될 거라고 기대되는 범위
- 즉, 표본으로 추정한 통계량이 모집단의 통계량에 포함된다고 기대하는 범위
- 결정한 신뢰수준 값으로 범위를 한정
- ✅ 신뢰구간 계산 방법
- 신뢰구간 = 표본평균 ± (z × 표준오차)
- 여기서 z는 선택된 신뢰수준에 해당하는 z-값입니다.
- ex, 95% 신뢰수준의 z-값은 1.96입니다.
- 일반적으로 95% 신뢰수준으로 설정
- 신뢰구간 = 표본평균 ± (z × 표준오차)
- 신뢰구간 메소드 : `scipy.stats.t.interval`
- interval(신뢰수준, 자유도, loc= 표본평균, scale= 표본오차)
▼ 신뢰구간 히스토그램 시각화 코드 구현
더보기
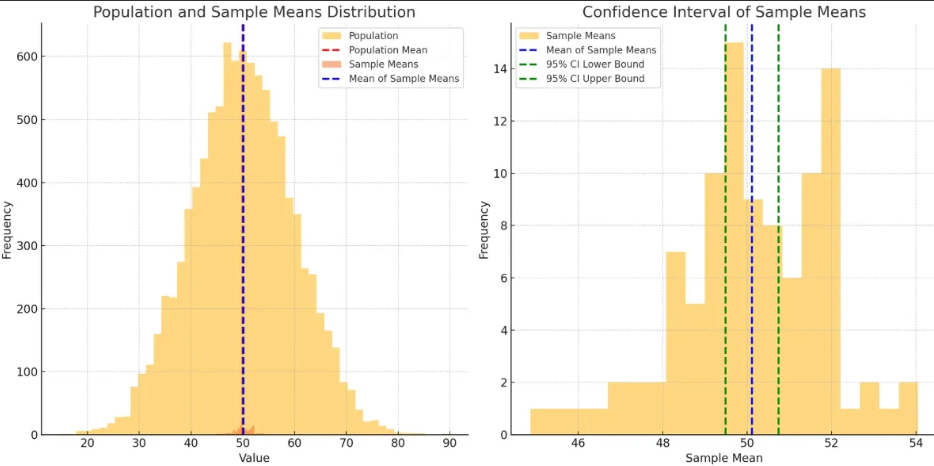
(좌측) 모집단의 평균 , (우측) 표본의 평균 & 신뢰구간(95%)
- 모집단의 평균과 표본의 평균 & 신뢰구간 히스토그램 시각화
- 모집단의 평균이 표본의 평균 신뢰구간 95% 범위안의 포함 되는가 ? yes
- zhem '

#수학점수 표본으로부터 모집단의 평균 범위를 계산해보자
import scipy.stats as stats
# 표본 평균과 표본 표준편차 계산
sample_mean = np.mean(sample)
sample_std = np.std(sample)
#신뢰구간 계산 : stats.t 분포로 95% 신뢰수준 계산
conf_interval = stats.t.interval(0.95, len(sample)-1, loc=sample_mean, scale=sample_std/np.sqrt(len(sample)))
print(f"표본 평균: {sample_mean}")
print(f"95% 신뢰구간: {conf_interval}")
#실제 모집단의 평균은 stats.t 분포로 가정했을때, 95% 신뢰구간은 이 범위 사이에 있음
#표본 오차 = 표준편차 / 표본크기의 제곱근
'통계,검정,머신러닝' 카테고리의 다른 글
| 연속 확률 분포 | 정규분포/ 표준 정규 분포/ 긴 꼬리 분포/ 스튜던트T 분포/ 카이제곱 분포 (0) | 2025.01.10 |
|---|---|
| 가설 검정 | Z검정과 T검정 ( +2표본 T검정 / SCIPY 모듈 코드) (0) | 2025.01.10 |
| 통계 기초 | 모수 추정과 가설 검정 (귀무가설/대립가설/검정 통계량/유의확률/유의수준/표준오차) (0) | 2025.01.09 |
| 이산 확률 분포 | 베르누이 분포, 이항 분포, 푸아송 분포 (+scipy 모듈) (0) | 2025.01.07 |
| 통계 기초 | 기술 통계와 추론 통계 (중심 경향치/ 산포도/ 상관 관계) (0) | 2025.01.06 |