➡️ 단순선형회귀 (Linear Regression)
하나의 독립 변수(X)와 하나의 종속 변수(Y) 간의 관계를 직선으로 모델링하는 방법 (변수가 한개)
* 회귀 분석 : 값을 예측, 경향성을 파악하기 위한 분석
- 적용 예시: 하나의 독립 변수에 변화에 따라 종속 변수의 변화를 분석하고 예측함
- ex. 광고비 x 와 매출 y 관계 분석
- 회귀식 ( 일차 함수)
- Y = β0 + β1X → y = ax + b
- 목표 : a (x의 계수) b(절편) 을 알아내야 함

- 단순 선형 회귀 : 파이썬 코드
더보기
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression -- 머신러닝 모듈
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
# 예시 데이터 생성
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 단순선형회귀 모델 생성 및 훈련 -- 학습
model = LinearRegression()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 회귀 계수 및 절편 출력
print("회귀 계수:", model.coef_)
print("절편:", model.intercept_)
# 모델 평가
mse = mean_squared_error(y_test, y_pred) -- 오차 (mse가 낮을 수록 좋음)
r2 = r2_score(y_test, y_pred) -- 스코어 (얼마나 잘 설명하는가 ? : r2는 높을수록 좋음)
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)
# 시각화
plt.scatter(X, y, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=2)
plt.title('linear regeression')
plt.xlabel('X : cost')
plt.ylabel('Y : sales')
plt.show()➡️ 다중 선형 회귀(Multiple Linear Regression)
두 개 이상의 독립 변수(X1, X2, ..., Xn)와 하나의 종속 변수(Y) 간의 관계를 모델링.
- 적용 예시: 종속변수에 영향을 미치는 여러 독립변수가 있을 때
- 다양한 광고비(TV, Radio, Newspaper)과 매출 간의 관계 분석.
- 현재의 광고비(TV, Radio, Newspaper)를 바탕으로 예상되는 매출을 예측 가능.
- 문제 : `다중공선성` 발생 가능성 있음
- 다중공선성(Multicollinearity)은 회귀분석에서 독립 변수들 간에 높은 상관관계가 있는 경우를 의미
- 즉, 변수들끼리 상관관계가 높은 경우,각 변수의 개별적인 효과를 분리해내기 어려워져 회귀의 해석이 어려움.
- 진짜 중요한 변수가 통계적으로 유의하지 않게 나올수도 있음
- 해결 ) 변수들간의 상관계수를 확인하여, 변수들간의 상관관계를 확인→ 주 성분 분석 (pca)으로 변수들을 효과적으로 줄임
- → 높은 계수를 가진 변수 중 하나를 제거
- 회귀식 ( 변수가 여러개인 일차 함수)
- Y = β0 + β1X1 + β2X2 + ... + βnXn

- 다중 선형 회귀 : 파이썬 코드
더보기
- 단순선형회귀와 코드 동일 ( + 데이터프레임)
# 예시 데이터 생성
data = {'TV': np.random.rand(100) * 100,
'Radio': np.random.rand(100) * 50,
'Newspaper': np.random.rand(100) * 30,
'Sales': np.random.rand(100) * 100}
df = pd.DataFrame(data)
# 독립 변수(X)와 종속 변수(Y) 설정
X = df[['TV', 'Radio', 'Newspaper']]
y = df['Sales']
# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 다중선형회귀 모델 생성 및 훈련
model = LinearRegression()
model.fit(X_train, y_train)
# 예측
y_pred = model.predict(X_test)
# 회귀 계수 및 절편 출력
print("회귀 계수:", model.coef_) -- 변수의 갯수만큼 리스트형으로 출력
print("절편:", model.intercept_) --1개
# 모델 평가
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)➡️ 범주형 변수와 분석법
- 수치형 데이터가 아닌 주로 문자형 데이터로 이루어져 있는 변수가 범주형 변수
- 순서가 있는 범주형 → 순번로 변환 [0,1]
- 순서가 없는 범주형
- 2개 : 임의의 숫자로 변환 [0 , 1]
- 3개 이상인 경우에는 무조건 `원-핫 인코딩` (하나만 1이고 나머지는 0인 벡터) 변환 → pandas의`get_dummies` 메소드 활용
- ex) 부산 = [1,0,0,0], 대전 = [0,1,0,0], 대구 = [0,0,1,0], 광주 = [0,0,0,1]
- 적용 예시 : 성별, 근무 경력과 연봉관의 관계 등
- `get_dummies` (원-핫 인코딩 메소드) : 범주형 변수 변환해주는 메소드
더보기
- pd.get_dummies(df, drop_first=True)
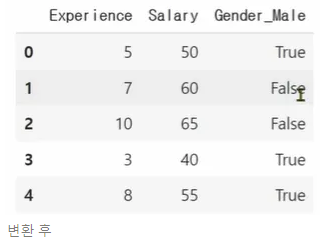
- drop_first=True : 범주형 2개일때 1개만(ex. 남성 여성이면 남성컬럼만) 생성해주는 옵션
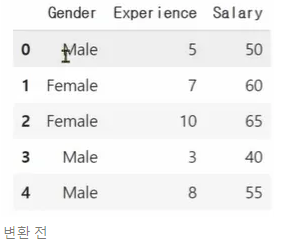
예시)성별 변환 ( male 컬럼 T/F + female 컬럼 T/F)


- 범주형 회귀 분석 : 파이썬 코드 (범주→ 더미 변수로 변환 후 회귀 분석)
더보기
# 예시 데이터 생성
data = {'Gender': ['Male', 'Female', 'Female', 'Male', 'Male'],
'Experience': [5, 7, 10, 3, 8],
'Salary': [50, 60, 65, 40, 55]}
df = pd.DataFrame(data)
# 범주형 변수 더미 변수로 변환
df = pd.get_dummies(df, drop_first=True)
# 독립 변수(X)와 종속 변수(Y) 설정
X = df[['Experience', 'Gender_Male']]
y = df['Salary']
# 단순선형회귀 모델 생성 및 훈련
model = LinearRegression()
model.fit(X, y)
# 예측
y_pred = model.predict(X)
# 회귀 계수 및 절편 출력
print("회귀 계수:", model.coef_)
print("절편:", model.intercept_)
# 모델 평가
mse = mean_squared_error(y, y_pred)
r2 = r2_score(y, y_pred)
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)➡️ 다항 회귀 (Polynomial Regression)
독립 변수와 종속 변수 간의 관계가 선형이 아닐 때 사용(비선형)
- 독립 변수의 다항식을 사용하여 종속 변수를 예측.
- 2차식 정도가 적절함
- 고차 다항식의 경우 과적합(overfitting) 위험이 있음
- 간단하게 말해서 추세만 보고 싶은데, 오차를 더 반영해서 보여주는 경우
- 적용 예시 :주택 가격 예측(면적과 가격 간의 비선형 관계)

- 다항 회귀 분석 : 파이썬 코드
더보기
*함수
PolynomialFeatures(degree=2) — 2차식 생성
polynomial_features.fit_transform(X)
PolynomialFeatures(degree=2) — 2차식 생성
polynomial_features.fit_transform(X)
from sklearn.preprocessing import PolynomialFeatures
# 예시 데이터 생성
np.random.seed(0)
X = 2 - 3 * np.random.normal(0, 1, 100)
y = X - 2 * (X ** 2) + np.random.normal(-3, 3, 100)
X = X[:, np.newaxis]
# 다항 회귀 (2차) -- 다항식 추가
polynomial_features = PolynomialFeatures(degree=2)
X_poly = polynomial_features.fit_transform(X)
model = LinearRegression()
model.fit(X_poly, y)
y_poly_pred = model.predict(X_poly)
# 모델 평가
mse = mean_squared_error(y, y_poly_pred)
r2 = r2_score(y, y_poly_pred)
print("평균 제곱 오차(MSE):", mse)
print("결정 계수(R2):", r2)
# 시각화
plt.scatter(X, y, s=10)
# 정렬된 X 값에 따른 y 값 예측
sorted_zip = sorted(zip(X, y_poly_pred))
X, y_poly_pred = zip(*sorted_zip)
plt.plot(X, y_poly_pred, color='m')
plt.title('polynomial regerssion')
plt.xlabel('area')
plt.ylabel('price')
plt.show()➡️ 스플라인 회귀(Spline Regression)
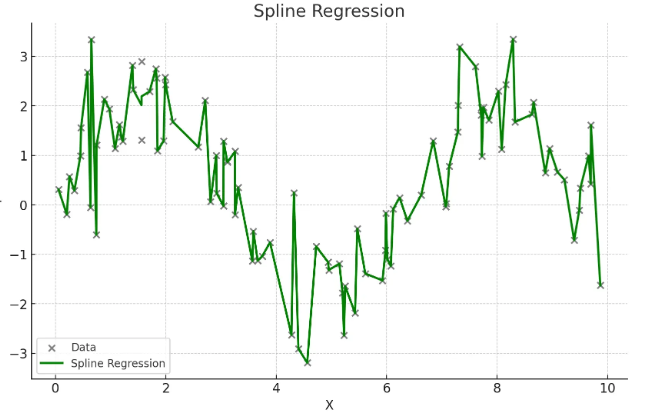
독립 변수의 구간별로 다른 회귀식을 적용하여 복잡한 관계를 모델링
- 구간마다 다른 다항식을 사용하여 전체적으로 매끄러운 곡선을 생성
- 적절한 매듭점(knots)의 선택이 중요
➡️ 회귀법 선택
- 선형성이 보일때 → `선형 회귀`
- 선형성이 보이진 않지만, 간단한 경향성은 보임→ `다항 회귀`
- 그 외 복잡한 관계 → `스플라인 회귀`
'통계,검정,머신러닝' 카테고리의 다른 글
| 머신러닝 | 머신러닝 기초와 선형 회귀 분석 (+sklearn 파이썬 실습) (0) | 2025.01.13 |
|---|---|
| 통계 기초 | 상관계수 (피어슨/스피어만/켄달 타우/상호정보 상관계수 / scipy & sklearn 모듈) (0) | 2025.01.10 |
| 연속 확률 분포 | 정규분포/ 표준 정규 분포/ 긴 꼬리 분포/ 스튜던트T 분포/ 카이제곱 분포 (0) | 2025.01.10 |
| 가설 검정 | Z검정과 T검정 ( +2표본 T검정 / SCIPY 모듈 코드) (0) | 2025.01.10 |
| 통계 기초 | 모수 추정과 가설 검정 (귀무가설/대립가설/검정 통계량/유의확률/유의수준/표준오차) (0) | 2025.01.09 |